Guaranteed Computation of Robot Trajectories
Simon Rohou, Luc Jaulin, Lyudmila Mihaylova, Fabrice Le Bars, Sandor M. Veres
Published in Robotics and Autonomous Systems, 2017 | Bibtex
Download the paper
Abstract. This paper proposes a new method for guaranteed integration of state equations. Within this framework, the variables of interest are trajectories submitted to both arithmetic and differential equations. The approach consists in formalizing a problem thanks to a constraint network and then apply these constraints to sets of trajectories. The contribution of the paper is to provide a reliable framework to enclose the solutions of these differential equations. Its use is shown to be simple, more general and more competitive than existing approaches dealing with guaranteed integration, especially when applied to mobile robotics. The flexibility of the developed framework allows to deal with non-linear differential equations or even differential inclusions built from datasets, while considering observations of the states of interest. An illustration of this method is given over several examples with mobile robots.
Keywords: guaranteed integration, tube programming, mobile robotics, constraints, contractors, ODE
Tube: definition
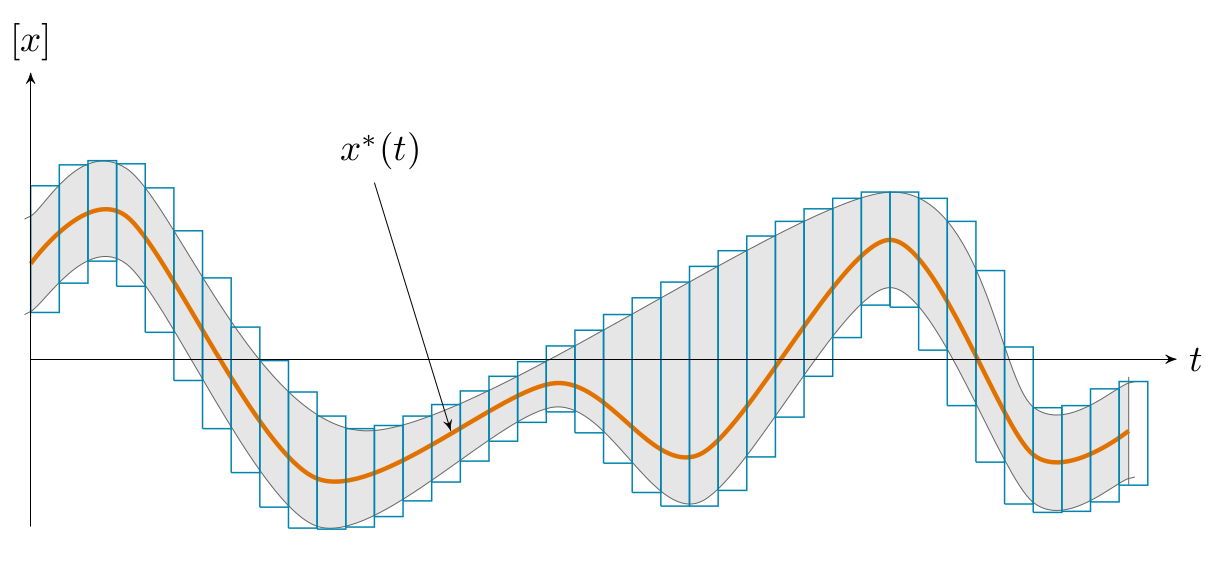
A tube is defined as an envelope enclosing an uncertain trajectory $\mathbf{x}(\cdot):\mathbb{R}\rightarrow\mathbb{R}^{n}$. In this paper, a tube $[\mathbf{x}](\cdot)$ is an interval of two trajectories $[\mathbf{x}^{-}(\cdot),\mathbf{x}^{+}(\cdot)]$ such that $\forall t,~\mathbf{x}^{-}(t)\leqslant\mathbf{x}^{+}(t)$. A trajectory $\mathbf{x}(\cdot)$ belongs to the tube $[\mathbf{x}](\cdot)$ if $\forall t,\mathbf{~x}(t)\in[\mathbf{x}](t)$. Figure 1 illustrates a tube implemented with a set of boxes.
Tubex library
Paper examples
Paper examples are available in the Tubex library:
Tube arithmetic
See: tubex-lib/examples/cpp/01_arithmetic
Causal kinematic chain (Dubin's car)
See: tubex-lib/examples/cpp/04_causal_chain
Lissajous example (multi-differential constraints)
See: tubex-lib/examples/cpp/05_lissajous